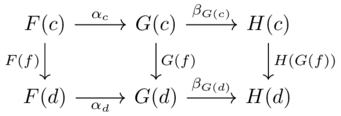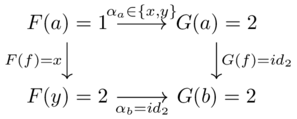Natural transformations

Natural transformation(1)

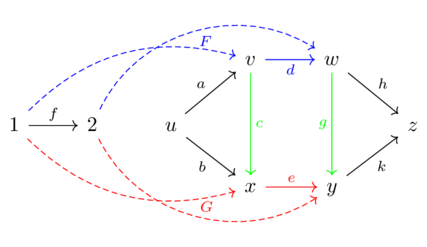
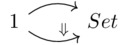
A natural transformation \(F \overset{a}\Rightarrow G\) between two functors (going from \(\mathcal{C}\) to \(\mathcal{D}\)).

For each object \(c \in \mathcal{C}\), one specifies a morphism \(F(c)\xrightarrow{\alpha_c}G(c)\) in \(\mathcal{D}\) called the c-component of \(\alpha\)
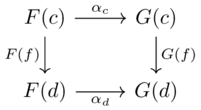
These components must satisfy the naturality condition: for each morphism \(c \xrightarrow{f} d\) in \(\mathcal{C}\) we need \(F(f);\alpha_d=\alpha_c;G(f)\)
AKA this diagram should commute:

Diagram(1)

A diagram \(\mathcal{D}\) in a category \(\mathcal{C}\)

A functor \(\mathcal{J}\xrightarrow{D}\mathcal{C}\) from any category \(\mathcal{J}\) called the indexing category of the diagram \(D\).
We say \(D\) commutes if \(D(f)=D(f')\) for every parallel pair of morphisms \(f,f'\) in \(\mathcal{J}\)

Functor category(1)

The functor category from categories \(\mathcal{C}\) to \(\mathcal{D}\)

\(\mathcal{D}^\mathcal{C}\) has all functors \(\mathcal{C} \rightarrow \mathcal{D}\) as objects and natural transformations as morphisms.

Small natural transformation example(1)

The natural transformation requires us to choose morphisms in the righthand category for each object in the lefthand category
The only choices to satisfy the naturality condition are ?\(c\) and \(g\).

Natural transformation to unit(1)

Just like sets are in bijection with functors \(\mathbf{1}\rightarrow\mathbf{Set}\), we can also associate ?natural transformations

with functions.
In the language of functor categories, this claim is to say \(\mathbf{Set}^1\) is equivalent to \(Set\).

Natural transformations between sequences(1)

Any non-decreasing sequence of naturals can be identified with a functor \(\mathbb{N}\rightarrow \mathbb{N}\), considering the preorder of naturals as a category.
A natural transformation between two of these functors would require a component \(\alpha_n\) for each natural, which means ?a morphism from \(F_n \rightarrow G_n\). This exists iff \(F(n)\leq G(n)\).
Thus we can put a ?preorder structure over the monotone map of \(\mathbb{N} \rightarrow \mathbb{N}\) (this is a thin functor category \(\mathbb{N}^\mathbb{N}\)).

Natural isomorphism of Bool-categories and preorders(1)

There exists a category PrO which has ?preorders as objects and ?monotone maps as morphisms.
There exists a category *Bool-Cat* in which the objects are ?Bool-categories and morphisms are ?Bool-functors.
We call these categories equivalent because there exist functors \(\mathbf{PrO}\overset{F}{\underset{G}{\rightleftarrows}}\mathbf{BoolCat}\) such that there exist ?natural isomorphisms \(F;G \cong id_\mathbf{PrO}\) and \(G;F \cong id_\mathbf{Bool-Cat}\)

Exercise 3-55(2)

Let’s investigate why the functor category is actually a category.

Figure out how to compose natural transformations \(F \xrightarrow{\alpha} G \xrightarrow{\beta}H\).
Propose an identity natural transformation on any functor and check that it is unital.

Solution(1)

?The individual natural transformations satsifying the naturality condition makes the left and right squares commute, meaning the whole diagram commutes:
- Thus the mapping from objects in \(F\)’s domain to morphisms in \(H\)’s codomain is given by ?\(G;\beta\).
Mapping each object to ?its own identity morphism will satisfy the naturality condition (all four edges of the square become identity functions). This will enforce unitality.

Exercise 3-58(2)

Let \(\mathcal{C}\) be an arbitrary category and \(\mathcal{P}\) be a preorder thought of as a category. Are the following true?

For any two functors \(\mathcal{C}\xrightarrow{F,G}\mathcal{P}\), there is at most one natural transformation \(F \rightarrow G\)
For any two functors \(\mathcal{P}\xrightarrow{F,G}\mathcal{C}\), there is at most one natural transformation \(F \rightarrow G\)

Solution(1)

This is true: there are no choices to be made for a natural transformation, given that for each morphism \(c\rightarrow d\) in \(\mathcal{C}\) we have to pick ?\(\alpha_c\) to be the morphism \(F(c)\rightarrow G(c)\) and ?\(\alpha_{d}\) to be the morphism \(F(d)\rightarrow G(d)\).
Counterexample:
- let \(F\) send \(f\mapsto x,a\mapsto1,b\mapsto 2\) and \(G\) maps everything to \(2\)
- The naturality condition for f leaves us with two choices for ?\(\alpha_a\)